本文转载自https://programmercarl.com/
3.
1. 数组
1.1. 滑动窗口
不断调整起始位置和终止位置,处理一块区间内的数据。
在本题中实现滑动窗口,主要确定如下三点:
- 窗口内是什么?
- 如何移动窗口的起始位置?
- 如何移动窗口的结束位置?
窗口就是 满足其和 ≥ s 的长度最小的 连续 子数组。
窗口的起始位置如何移动:如果当前窗口的值大于等于s了,窗口就要向前移动了(也就是该缩小了)。确定好移动的情况,并处理需要优先移动窗口还是先处理窗口中的数据。
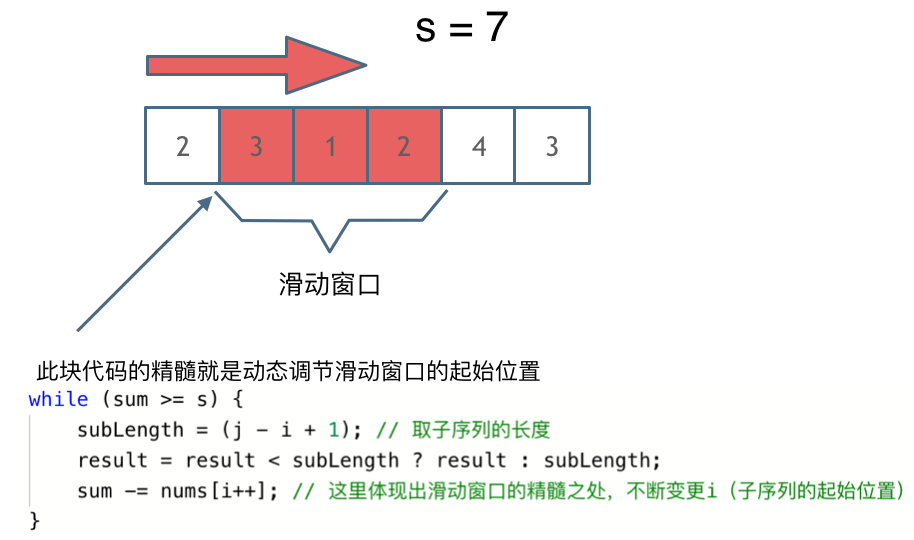
窗口的结束位置如何移动:窗口的结束位置就是遍历数组的指针,也就是for循环里的索引。
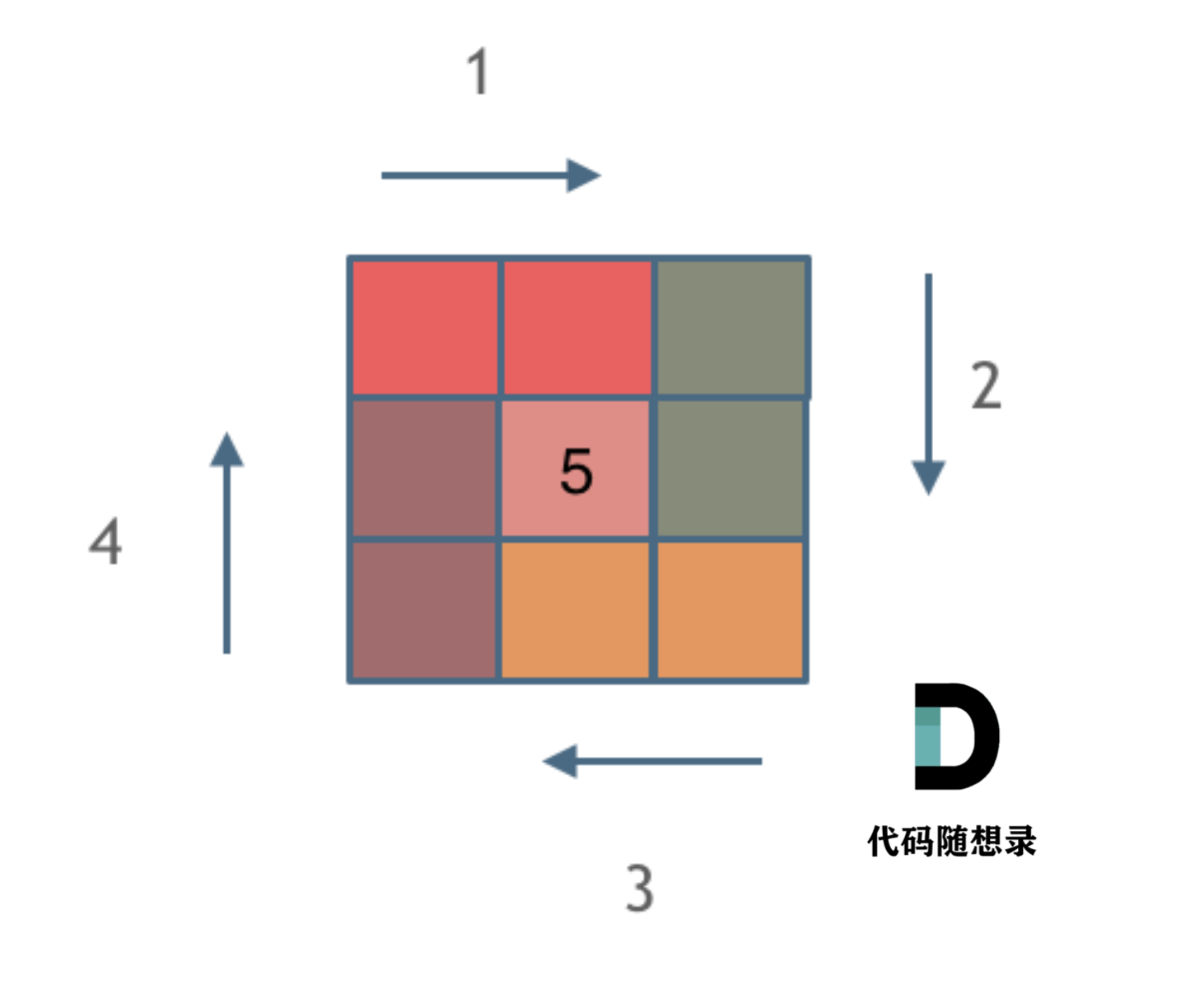
1.2. 螺旋数组
确定边界处理的不变量,确保每个子问题的结构都是相同的
每画一条边都要坚持一致的左闭右开,或者左开右闭的原则,这样这一圈才能按照统一的规则画下来。
左闭右开后,每次处理n-1个数据,每减少一圈,处理数据-1
1.3. 唤醒链表
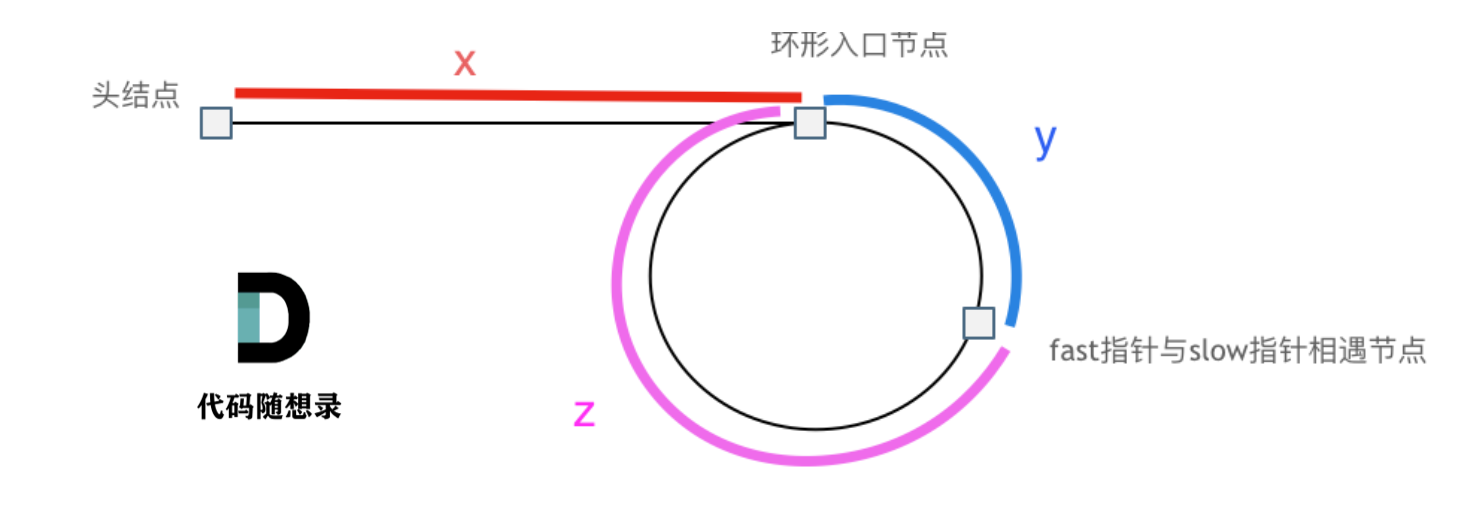
$$
slow = x+y \
fast = x+y+n(y+z) \
fast = 2slow
$$
计算得到
$$
x = (n-1)(y+z)+z
$$
代表,*从头节点走向环形入口 = 从相遇点出发走n个节点
// 先向前走再进行验证,否则第一个就相等了
1.4. 前缀和
将之间计算的结果累加保存在数据中,之后使用时使用结算完成的数组
需要更具题目要求,选择计算什么样的前缀数组
while (~scanf("%d%d", &a, &b))//按位取反,如果结果是eof=-1,取反之后结果为0
重大发现:scanf与printf处理数据比cin,cout速度更快
这是一篇测试文章


就当是没有图片了吧,在本地无法显示的图片,在博客中显示了。
1.5. 哈希表
1.5.1. 数组作为哈希表
1.5.2. stl中的哈希表
此时就要使用另一种结构体了,set ,关于set,C++ 给提供了如下三种可用的数据结构:
- std::set
- std::multiset
- std::unordered_set
std::set和std::multiset底层实现都是红黑树,std::unordered_set的底层实现是哈希表, 使用unordered_set 读写效率是最高的,并不需要对数据进行排序,而且还不要让数据重复,所以选择unordered_set。
1.6. 回溯算法
算法的模板
void backtracking(参数){
if(终止条件){
存放结果;
return;
}
for(选择:本层集合中的元素){
处理节点;
backtracking(路径, 选择列表); //递归
回溯,撤销处理结果;
}
}
vector
a a.push_back(int b) 压入数据, a.pop_back(), 弹出数据
还可以采用insert, + ,压入数据,使用erase(begin()+ i ,end())弹出数据
使用切割时候,需要注意下一次开始为本次切割后的下一次位置,此处回溯时候不需要还原,其余元素均需要还原。还原时候注意还原的位置。
1.6.1. 分割字符串方法
- 函数传递,参数
s + start + end - 使用string 切割,
string s = s.substr(start, end)
1.6.2. 两阶vector初始化方法
is_palind_rome.resize(s.size(), vector<bool>(s.size(), false));
2. 图论
2.1. 图查找算法
2.1.1. 并查集的实现 并查集理论基础 | 代码随想录
- 并查集,是将一个集合内所有数据放入一个连通图中,即为father[u]= v;
- 查询一个并查集,是查询根节点是否相同,find(u)== find(v)
- 初始化,所有的并查集都指向自身
- 路径压缩,节点在find过程中都执行根节点
// 使用数据存放并查集
vector<int> father(n, 0);
void init(){
for(int i = 0;i< father.size();i++){
father[i]= i;
}
}
int find(int u){
if(father[u]==u) return u;
else {
father[u]=find(father[u]);// 路径压缩,指向根节点
}
return father[u];
}
int is_same(int u, int v){
int a = find(u);
int b = find(v);
if(a == b) return 1;
else return 0;
}
void join(int u, int v){
int a = find(u);
int b = find(v);
if(a == b) return ;
father[u]= v;
return ;
}
2.1.2. prim算法
- 选择最小边e,v(e是树中,v是树外的数据)
- 将节点v加入树中
- 更新与v的节点的权重
- 此处记录树的连接关系,记录当前节点的父亲
2.1.3. kruskal 算法
- 完成并查集
- 对边的权重排序
- 选择最小边
- 如果在并查集中,跳过
- 不在并查集中,加入节点树种
2.1.4. 拓扑排序
- 计算节点入度
- 选择入度为0 的节点,加入处理队列q, 并将入度替换为-1
- 处理队列q
- cur指向的所有节点,入度减1
- 如果入度等于1,加入处理队列q, 并将入度替换为-1
- 记录出队元素cur.
出队元素不等于总元素数量时, 判断有向图中 存在环
2.1.5. dijkstra算法
权值不能为负数,prim算法权值可以是负数,负数情况使用ford算法
- 选择最小边并且该节点没有被访问过
- 标记该节点,已经被访问过
- 更新非访问节点到源点的最小距离,同时当前节点的父亲
2.1.6. 使用边权重的dijkstra算法
使用边的权值进行计算
- 建立小顶堆
- 从小顶堆中选择最小的边
- 标记边连线的点已经被访问过了
- 更新edge相连的顶点的权重
2.2. 附录
2.2.1. 建立小顶堆
#include <queue>
class mycomparison{
bool operator(const pair<int, int>& a, const pair<int, int>& b){
return a.second> b.second;
}
}
priority_queue<pair<int, int>, vector<pair<int,int>> , mycomparison> p;
/*
a> b时 ,是小顶堆;
a< b时, 是大顶堆;
*/
2.2.2. 对vector数组进行排序
#include <algorithm>
vector<int> edges;
sort(edges.begin() , edges.end(), [](const edge& a, const edge& b){
return a< b;
});
/*
a< b, 升序排序;
a> b, 降序排序;
默认情况是升序排序;
*/



