栈-队列

1. 栈

感谢代码随想录

1.1. 栈模拟队列

模拟队列

232.用栈实现队列版本2

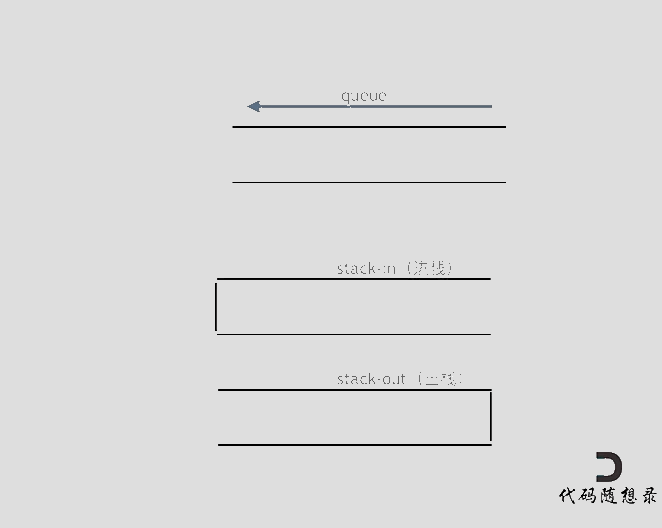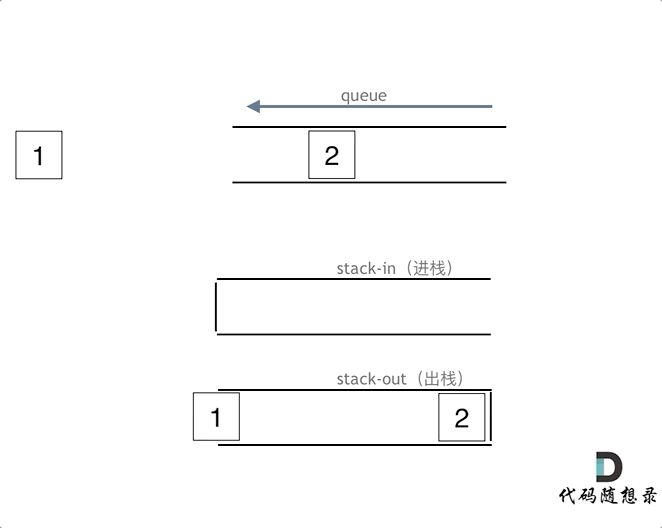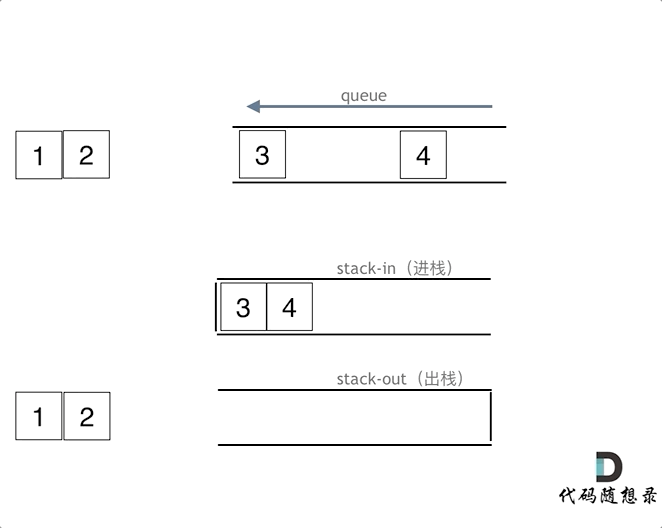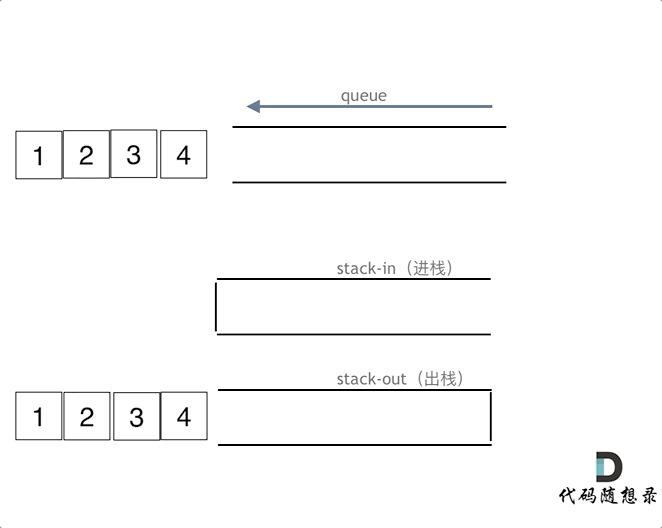
使用两个栈模拟队列

1. 入队时， 直接入队
2. 出队时， 将输入栈的数据放入输出栈中，将顺序倒置为先入先出
3. 判空时，需要判断两个栈是否为空

1.2. 栈队列排除元素

含有退格的字符串

题目中遇到i元素， 需要退回i-1的元素时，可以使用栈弹出i-1元素

1.2.1. 双指针法

slow , fast 从后向前比较

1. 元素相同，同时向前
2. 遇到# ，slow / fast 向前
3. 否则， 返回false

2. 队列

2.1. 队列模拟栈

225.用队列实现栈

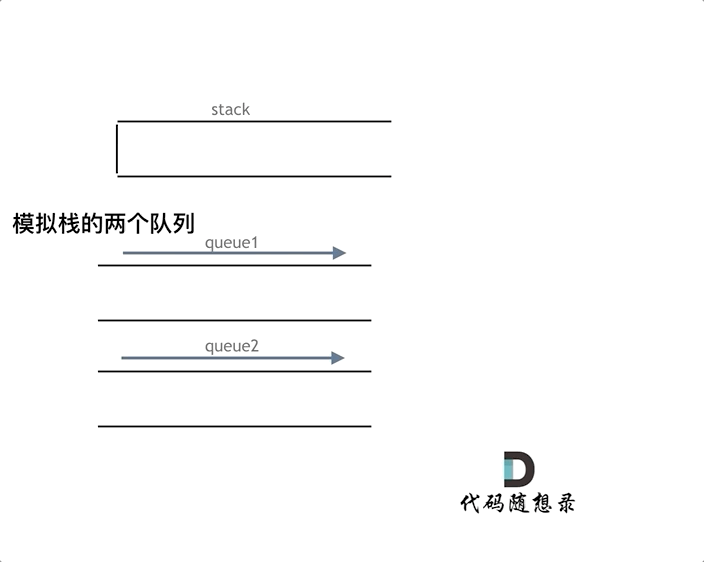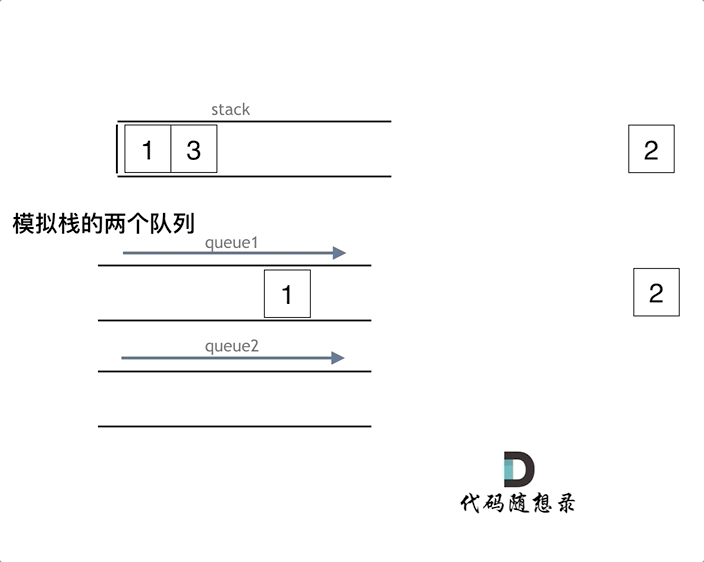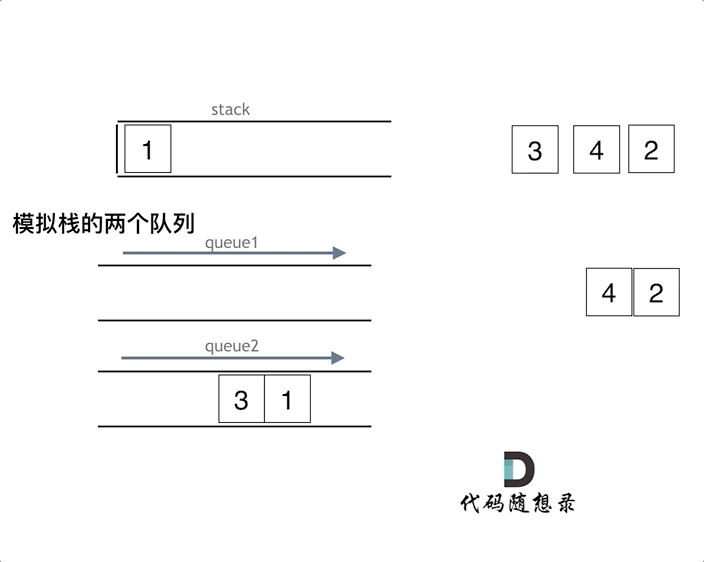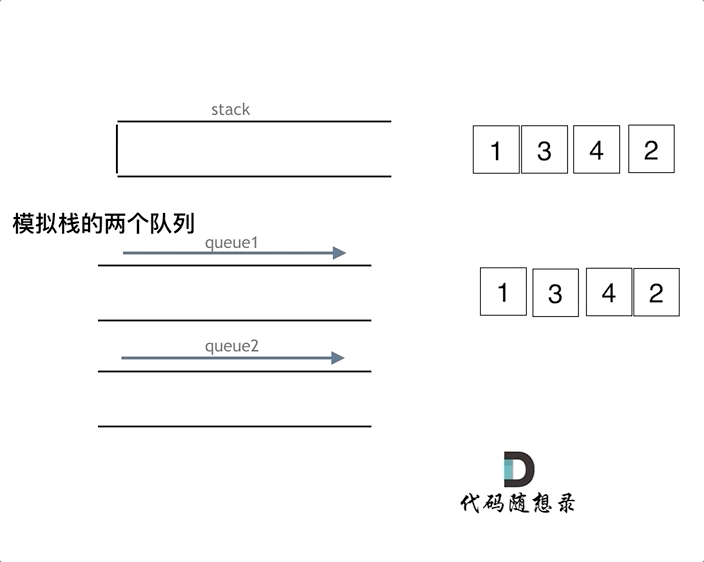
可以使用一个队列实现栈的模拟

1. 入栈时，直接入队
2. 出栈时，需要将前置数据依次排出，并放置在队首，出队时需要保留最后一个元素出队

2.2. 滑动窗口最大值

滑动窗口最大值

deque 用法

#include <deque>
deque<int> d;
d.front(), d.back();
d.push_back(), d.pop_back();
d.push_front(), d.pop_front();

构建排序队列，将可能的最大值放入队列中，定义新的队列弹出方法

1. 入队，入队值如果大于栈顶值，将栈顶出栈，直到入队值小于栈顶值
2. 出队，队首值如果等于移除的数据，将输出出栈
3. 保持第一个值是最大值a，且比a小的值是在a之后入栈的，所以出队时a之前的数据已经弹出完毕

2.3. 优先队列

前k个高频词汇

priority_queue需要自定义排序类型

1. 使用` bool operator()(const int& a, const int& b)自定义比较类型
2. 快排中left> right，从大到小，优先队列反过来

class mycomparison{
    public:
    bool operator()(const pair<int, int>& a, const pair<int, int>& b){
        return a.second > b.second;
    }
};
priority_queue< pair<int, int>, vector<pair<int, int>> , mycomparison> q;

使用小顶堆，优先排除较小元素，将较大元素保留在优先队列中。

3. 单调栈

3.1. 右侧最高气温

最高气温

查找右边 比 当前元素更小的元素

1. 右边比自身大，找到了，当前元素出栈
2. 右边比自身小，没找到，入栈

栈中元素为待查找的元素，找到了就出栈

3.2. nums1元素在nums2中下一个最大元素

nums1元素在nums2中下一个最大元素

1. 先计算num2中下一个更大元素的结果，保存在map中
2. num1从map中取得结果

3.3. 循环数组的下一最大元素

循环数组的下一最大元素

nums是一个循环数组，最后一个元素接在第一个元素

1. 对数组循环时， 使用 % nums.size() 对数组循环遍历
2. 遍历次数增加一倍，从1遍历到 2*n

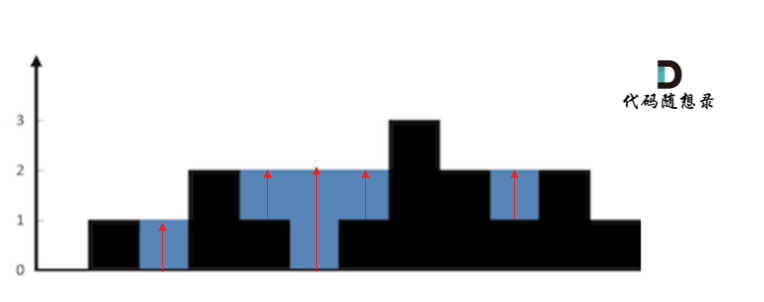
3.4. 接雨水

接雨水

左边和右边高度高于中间时，中间出现凹槽， 可以接到雨水

3.4.1. 暴力求解

当前节点j

1. 左边[0,j-1]最大高度lheight,右边[j+1 , end]最大高度rheight，每次暴力求解这两个指针

2. 计算高度差，使用列方向计算求和

   

3.4.2. 动态规划

1. j左边最大高度 = j-1左边最高高度，或者height[j-1]
2. 右边计算公式为 rheight[j] = max(rheight[j+1] , height[j+1])

先计算出dp， 代替暴力求解 中的双指针

3.4.3. 单调栈

单调递增栈中，栈底 > 栈头

如果出栈j， 栈头元素> j, 即将入栈元素 > j， 出现凹槽，计算这个凹槽

宽 = 入栈元素 - 栈顶元素， 高度 = min(入栈， 栈顶) - 出栈元素(凹槽)

行计算