图论

1. 图论 搜索

感谢代码随想录

1.1. 图论基础

1.1.1. 邻接矩阵

邻接矩阵使用二维数组保存信息，矩阵中每个节点代表一个元素

typedef struct Node{
    int data;
}Node;
typedef vector<vector<Node>> Graph;

1.1.2. 邻接表

邻接表—— 一个节点连接中存在弧 节点的首指针

// 弧节点信息
typedef struct arc{
	int info;
	struct arc* next;
}arc, *acrlink;

// 节点信息，包含弧节点首指针
typedef struct Node{
    int info;
    arclink* firstArc;
}Node,Nodelink;

// 使用数组存放
typedef vector<Node> Graph;

// 使用链表存放
typedef link<Node> Graph;

1.1.3. 有向图

有向图的边(a, b)， 其中只存放 a->b的边

1.1.4. 无向图

无向图的边(a, b), a 节点中存放一条a->b的边， b节点存放一条 b->a的边

1.1.5. 连通分量

无向图中 能够从一个节点到所有的节点的 最大子图

123 是连通分量， 12不是连通分量

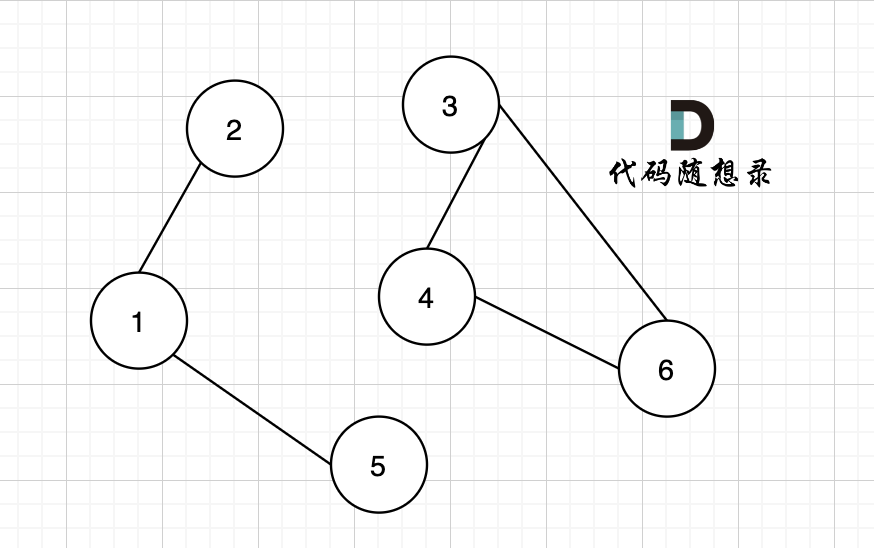
1.1.6. 强连通分量

有向图中， 增加了方向，依旧是连通分量成为强连通分量

1.1.7. 弱连通分量

有向图中，增加了方向，不是连通分量 ； 减少方向，是连通分量，是弱~；

img

1.2. 岛屿数量

1. 每次遍历可以得到一个连通分量， 遍历总次数 = 所有连通分量= 岛屿数量
2. 使用visited 数组标识 已访问节点

1.2.1. 深度搜索dfs

1. 中止条件：

   1. 节点访问过 ，visited[i][j] = true
   2. 节点没有相连，g[i][j] = 0

2. 处理逻辑：

   1. 开始对其节点遍历，将其标识为true

   2. 对所有相邻节点遍历

      图中相邻节点是其上、下、左、右坐标

   3. 对节点遍历之前需要对节点坐标进行检查

3. 返回值，没有返回值

1.2.2. 广度搜索BFS

1. 取出队列首元素，将其所有相邻节点加入队列中，依次遍历，直到队列中元素为空

2. 使用visited 数组标识遍历过的节点

   1. 在加入队列时，标记已访问

      加入队列时没有标记， 出队列时标记，下一个访问当前节点会再次放入队列中，多次遍历

      

      img

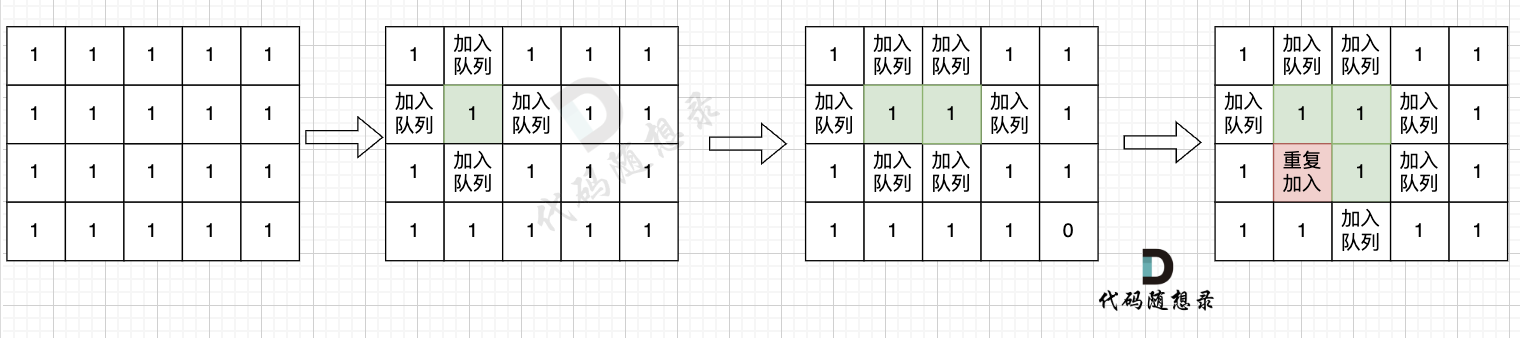
1.3. 岛屿的最大面积

一次遍历 = 一个连通分量= 一个岛屿， 统计每次遍历过程中的最大遍历节点数量

写if-else时， 尽可能把结果都包含在内，没有操作时再不写

1. 有节点遍历时，节点数量 +1
2. 没有节点遍历时，节点数量初始为0

1. dfs
   1. 优先处理节点，进入函数后，首先操作本节点， count初始为0
   2. 优先处理相邻节点，须在进入下一节点时，就将下一个节点处理，count 初始为1
2. bfs，只有在加入队列时处理，处理的是当前节点，初始化为0

1.4. 孤岛的最大面积

孤岛 = 四周没有与图的边沿相连

1. 将所有与陆地相连的岛都置为海洋
2. 计算剩下岛的面积

两个边沿， 从四个边沿开始遍历，遍历的节点置为0，使用grid作为标识，此时可不用visited

1. [0][i], [n-1][i]
2. [i][0], [i][m-1]

1.5. 水流问题

求出能流向低处的节点

1. 暴力求解，求当前节点能否到达 边界
2. 逆推， 从边界向上推，看左边界能到的哪些节点firstBoard，以及有边界secondBoard
3. 左右边界都能到达，为逆推结果

1.6. 建造最大岛屿

海洋中造出一块岛， 连接其他岛屿，组成最大面积

1. 首先统计每个岛屿的面积，并为每个岛屿附上标识，并建立标识对应的面积

   建立标识后，可以标识当前节点已被访问，可以用这个标识代替visited

2. 统计 0 值附近所有岛屿面积的和，不同的岛屿需要去重

3. 比较出最大值

1.7. 岛屿的周长

岛屿与海相邻的周长

岛的陆地是一个正方形，每一条边，与海洋相连都是陆地周长，因此可以使用图论的方法，而不是总时搜索

1. 陆地地界的边沿是有一块海洋，边长加1

   矩阵边沿也是海洋，也要统计

2. 每两块相邻的陆地都需要减去2个边沿，= 每相邻一块陆地，需要减去一个边沿

   统计所有陆地sum,总边数4*sum ，统计相邻陆地数cover,减去边沿cover

   陆地边沿 = sum*4 - cover

1.8. 字符串接龙

字符串作为路径，广度搜索

字符串接龙是无向图

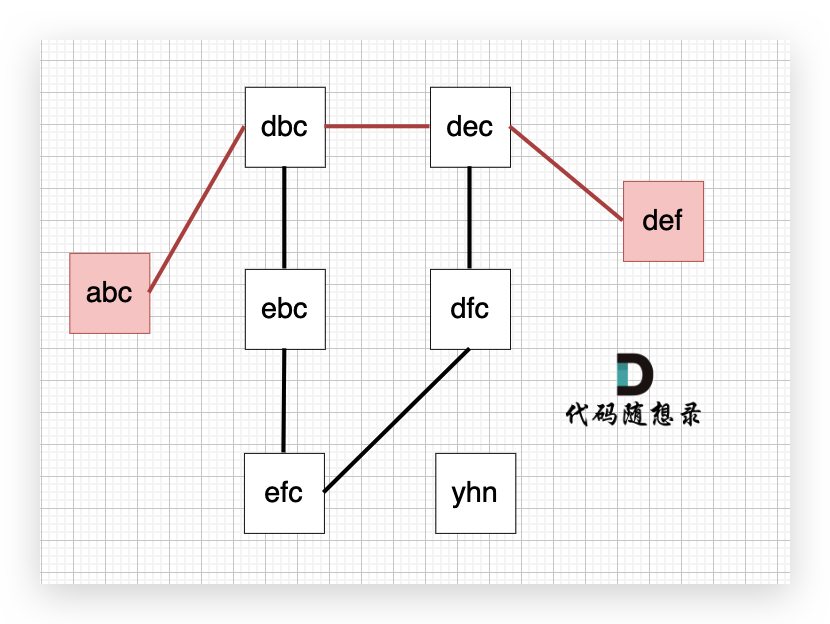
1. 无向图中可以使用广度搜索，找打目标节点，即为最短路径
2. 遍历时需要使用visited标识节点，避免循环，此时visited可以使用set标识，也可以使用map，同时标识走到这里的最短路径
3. 对字符串的替换是对图可行路径的查找，找到了在集合中，标识找到了一条可行路径

1.9. 邻接表遍历

邻接表中是以，节点作为数组元素，同时还有节点后指向 一个链表，指向与节点相连的节点

vector<list<int>> g(n+1)，以数组序号作为节点元素，数组的list作为相邻链表

// 深搜和广搜中都需要对相邻节点的列表进行遍历
// list的遍历方法

//1. 指针
for(auto it = list.begin() ; it !=  list.end() ; i++){}

// 使用遍历
for(auto i : list){}
// 不能使用类似vector 的for(int i = 0 ; i < vector.size() ;i++){}，list不能使用下标去访问

2. 算法

2.1. 并查集

含义： 一个集合中的元素指向同一个根节点， 根节点指向自身

1. 初始化，所有节点指向自身
2. 插入时，将节点 -> 该集合的根节点
   1. 如果是集合 插入 集合， 需要将集合 的根节点 指向 另一个集合的 根节点
3. 比较时，比较两个元素的根节点是否相同
4. 查找， 迭代查找根节点(指向自身的 节点)
   1. 并查集的缩小： 在查找到根节点时， 将当前元素的父节点指向根节点，减少深度，加快查询

n = 1000;
vector<int> father = vector<int>(1000, 0);

void init(vector<int>& father){
    for(int i = 0 ; i< father.size() ; i++){
        father[i] = i ;
    }
}

void find(vector<int> father, int u  ){
    if( u == father[u]) return u;
    else{
       	int u_father = find(father[u]);
        father[u] = u_father;
        // 简化为 father[u] = find[u]
        return u_father;
    }
}

bool isSame(vector<int> father, int u,  int v){
  	int u_father = find(u);
    int v_father = find(v);
    return u_father == v_father;
}

void join(vector<int> father, int u , int v){
    int u_father = find(u);
    int v_father = find(v);
    if(u_father == v_father) return ;
    // 注意这里插入时，插入的是根节点，不是将u,v 插入
    else father[v_father] = u_father;
}

2.2. 无向图中是否有路径

1. 将所有的节点加入并查集中
2. 查看节点i, j 是否重复出现在并查集中，如果是，那就有路径

2.3. 无向图中冗余连接

1. 如果边i, j 冗余，=》 顶点i,j之前就插入在并查集中，具有相同的根
2. 删除最后一个并查集相同根 的 两个节点组成的边

2.4. 有向图中的冗余连接

与无向图 不同，有向图冗余边有以下情况：

1. 入度为2 的节点， 一定会有两个边，删除其中1条
2. 如果删除只有还是一个树 ， 这条边可以删除， = 所有节点可以组成并查集
3. 如果不能构成树，那一定是一个环， 这个边就不是应该删除的边，应是零一条边
4. 如果没有入度为1的节点，一定是有环图
   1. 将节点依次加入并查集中，删除最后一个形成环的节点

删除冗余的最后一条边

1. 成环的最后一条边 -> 最后使得并查集冗余的边
2. 节点度为2的边，二选一，选择最后一个插入列表的进行判断

2.5. 最小生成树

2.5.1. prim

算法步骤：

初始化： minDist中默认权重不要超过 最大值，否则无法选择节点

1. 选择距离最小生成树最小的节点
2. 将节点加入树中
3. 更新其他节点到最小生成的距离

使用数据结构minDist 保存节点到当前生成树的最短路径，

• 最终， minDist中保存着最小生成树的权值
• isTree 记录当前节点是否在树中
• parent 记录与其相连的节点， 记录生成树边

2.5.2. kruscal

对所有边操作，之前邻接表，邻接矩阵都是对顶点的描述，这里需要定义关于边的数据结构

typedef struct edge{
    int e1;
    int e2;
    int w;
}Edge ; 

1. 将所有边保存
2. 按照权重对边，从小到大排序
3. 对所有边遍历
   1. 在同一个并查集中，跳过
   2. 在不同集合中，加入结果，并加入在同一个并查集中

2.6. 拓扑排序

topology_sort

对于一个给定的有向图，转换为线性的排序； 图中有环时，不能做线性排序

=> 节点入度为0 的时候，没有依赖，选择作为结果

• 拓扑排序可以用于有向图 无环判断
• 无向图的环判断可以使用并查集判断

1. 统计所有边入度， a->b， 统计b节点的度

2. 选择度为0 的节点，加入待处理集中，可以使用queue作为待处理

3. 删除节点i，并将其加入结果集中

   删除节点i，是删除与其相邻的节点，此时入度为0 ，只有i->j的边，将节点j入度 -1 即可

3. 最短路径

3.1. 单源最短路径Dijkstra

选择 节点i 到原点的最近距离

prim 寻找节点i到生成树的最近距离，原理相同，不过minDist存放值不同1

1. 选择距离源点最近的节点

   dijkstra 的源点到 源点的距离为0，初始化源点为0

   prim 初始树没有生成，初始节点均为INT_MAIX-1(方便选择第一个节点)

2. 将节点插入结果集中，标志为已访问

3. 更新节点相邻节点 的 minDist

借助三个数组：

1. minDist[j]: j到源点的最小值
2. visited[j]： j是否已找到最小值
3. parent[j]: 与j相连的父节点，每次更新最小值时，更新

3.1.1. 使用边进行Dijkstra

其中有两处修改

1. 使用邻接表代替邻接矩阵

2. 使用堆排序选择 距离源点最近的节点

   cur = q.top() ;// 最小的距离节点
   q.pop();

   替换掉使用for对minDist的遍历，查找最小距离节点

3. 遍历中，使用对边遍历，代替对节点遍历，

   while(!q.empty()) // 所有的边都保存在q中

修改之后使用的数据结构：

1. priority_queue<Arc, vector<Arc> , greater<Arc>> 对边权重的小顶堆

小顶堆中a < b，需要使用 >

1. 重定义Arc中的> ，使其能够 >比较运算

2. 使用greater ，使用>

   也可以重定义一个比较类，替换2

比较类写法：

class Arc{
public:
    int node;
    int w;
    // > 紧跟在operator之后
    // 参数使用 const + &
    // 函数需要使用const 
    bool operator>(const Arc& other) const{
        return this->w > other.w;
    }
}; 

3.2. Bellman-ford算法

可以用于解决具有负权边的结果 ， 对边进行缩放，此时可以只存储边

dijskra不能处理具有负权边的结果， 使用的是贪心算法，选择当前最近的边，对 负权边忽视最优结果

Bellman-ford算法类似于动态规划的算法， minDist[i] = min(minDist[i] , minDist[j-1] + value),

通过n-1 次迭代， 一定能找到最小边

1. 遍历n-1次

2. 对所有边进行一次修改，每次修改更新最小边

   如果from 节点 = INT_MAX ，没有到达from 节点，此时不修改MinDist结果

3.2.1. 动态规划思想

dp[k][j] 是最多 k条边经过的最短路径，有两种计算结果

1. 刚好k次到达最短路径，dp[k-1][v] + weight， v是能到达 j的节点
2. 前k-1次已经到达最短路径， dp[k-1][j]

dp[k][j] = min(dp[k-1][j] , min(dp[k-1][v]))

3.2.2. Bellman-ford 队列优化算法

边i-j 中，只有minDist[i] 的权重发生改变，相邻的minDist[j]才需要发生改变， 与i相邻的所有节点都需要更新，此时使用邻接表存储图效果最好

此时，使用队列queue存放节点i， 作为待处理节点

同一节点可能未处理之前，可能被修改对此，因此使用visited数组，标识节点是否在队列中，在队列中不需要重复加入

注意： 优化算法只对较少边的情况进行优化， 如果边的数量较多时，优化算法因为queue操作不适合优化

3.2.3. Bellman-ford 判断负权回路

判断是否有回路，且值为负数权重

1. 由Bellman_ford算法原理 中， 松弛n-1次后， minDist结果不再发生改变
2. 所有再多遍历一次，如果在第n后，还发生改变，那么一定出现了负权回路

3.2.4. 有限制的最短路径

从i- j 限制经过k个节点 = 可以经过k+1条边

minDist经过k轮松弛，得到最大长度为k的最短路径， 因此原题 = 经过k+1次最短路径得到的结果

但是由于算法采用了滚动数组， 导致第i条边应在第i轮更改，却在之前轮数中，修改，因此需要保留上一轮的数据，下一轮必须使用上一轮进行修改，保证结果正确性。

1. 使用缓存数组 存放 上一组中的最短路径
2. 下一组计算时，需使用上一组的数据进行修改

3.2.4.1. DP 求解

1. dp[i][j] 标识经历i条边，到达第j点的最短路径

2. dp[i][j]的计算方式

   1. 不经历 第i条边，可以到达j点， dp[i-1][j]
   2. 经历第i条边，遍历所有from->j的边, 因from是到达的第i-1条边， 结果为dp[i-1][from] + w

   两者最选择，取最小值

3. 初始化，起始节点第0轮一定为0，其余初始化为INT_MAX,便于遍历

4. 遍历顺序： 第一轮迭代次数 = 经历k条边，第二轮遍历所有节点即可

3.2.4.2. 使用queue优化

最主要问题： 统计迭代次数，并且使用上一次的计算结果算本次的更新结果

1. 使用old_minDist, q_size在每次迭代之前，统计上一次的迭代结果
2. 结束上一次迭代中待更新的所有节点后，停止本次迭代， 迭代数量-1， 统计下一个迭代

3.3. 多源最短路径算法Floyd

算法可以同时计算出多个起源到各个终点的距离，使用动态规划的思想

1. dp[i][j][k] 节点i -> j经过经过[0,k]中节点的最短路径

2. dp[i][j][k] 中i->j最短路径有两种计算方法：

3. 经过k节点， 即分为两段i->k->j， 计算公式为dp[i][k][k-1] + dp[k][j][k-1]

4. 不经过k节点，从k-1节点经过，计算公式为dp[i][j][k-1]

   从中选择最优方案，min(1, 2)

5. 初始化：

   1. dp 有k=0时计算，初始dp[i][j][0]，经过0个节点，即为初始图路径值
   2. dp[i][j][0]其余边初始为最大值，便于比较出最小值

6. 遍历顺序：

   1. k层计算依赖于k-1，所有优先计算出k-1层，k在第一层，从小向大遍历

4. 搜索算法

4.1. A*算法

1. 设计启发函数，由启发函数计算值为节点的选取增加权重
2. 每次选择节点时，依照权重选择节点

使用A*算法优化广度搜索算法(还可以优化Dijkstra算法)，

广度搜索算法，每次出队相当于取出节点，在这里为出队的节点增加权重，每次出队按照权重低的出队

1. 建立优先队列，从小到大排序，每次取出权重最小的节点
2. 每次加入队列时，计算启发函数作为权重值