OR 导论

1. intruction

问题 - 》模型 - 》 算法

1.1. 原理 ARRD

• A - approximation ， 近似求解
• R - reformulation , 对问题进行重构
• R - relaxation , 对复杂约束进行处理 - 线性松弛
• D - Decomposition, 大规模问题分割子问题

2. 线性导论

所有的向量都需要使用 mathbf 加粗， 且向量均为列向量

$$\mathbf{a}$$

类型	表示方法	展示
标量	普通	$x$
向量	粗体小写字母，使用 \mathbf	$\mathbf{x}$
矩阵	粗体大写字母，使用 mathbf	$\mathbf{X}$
张量	花体字母， 使用 \mathcal	$\mathcal{X}$

2.1. 单纯形法

性质：最优点一定在顶点 / 无穷点 上

1. 从一个顶点开始
2. 判断是否是最优点，stop， 否则进入 3 中
3. 如何移动到相邻顶点

顶点是由两条边相交形成的，然后形成一个顶点，作为待解点

2.2. stardard form

1. 最小化目标函数
2. 等式约束
3. 变量非负

$$\begin{aligned} & \min c^T x \\ & s.t \quad \mathbf{A}\mathbf{x} = \mathbf{b}\\ & \quad x \geq 0 \end{aligned}$$

使用乘法，按照元素方式看待模型

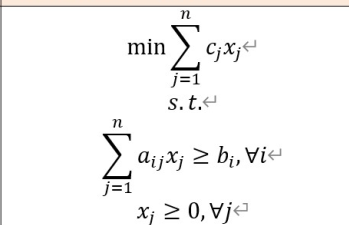
2.3. converting to stardard

2.3.1. 目标中存在绝对值

使用 $x^+. x^-$ 来替换|x|

按照更换公式, $|x| , x$ 的表示方法如下：

$$|x| = x^+ + x^- \\ x = x^+ - x^-$$

2.3.2. 不等式转换为等式

增加 松弛变量

1. 小于时， 加上松弛变量
2. 大于时， 减去松弛变量

2.3.3. 最大化 - > 最小化

增加 “-”

$$\max c^T x = -min -c^T x$$

2.4. 凸函数

凸函数定义：开口向上，具有最小值

2.4.1. 性质

1. $f_1, f_2, \dots, f_n$ 都是凸函数 $y = max(f(x))$ 也是凸函数

2. 一堆线性函数求最大值，是凸函数 ，

   $$\max\limits_{i = 1 ... m }{c^T x + b }$$

   一个凸函数可以转换为多个分段线性函数

   

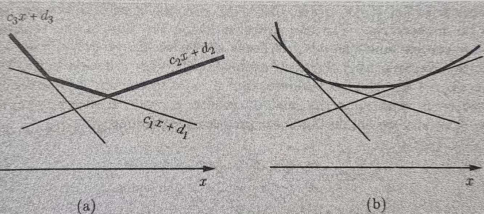
使用多个线性的 max 表示之后，可以使用引入新变量，消除 max

max 可以引用一个新的变量替换

|X| = max{x, -x }

2.5. linear algebra

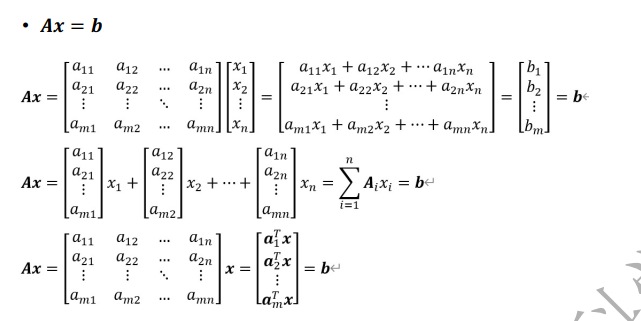
3. 几何表示

一个等式 是 一个超平面（对应维度的子空间， 少一个维度的空间）

可以叫对应的几何空间划分为三个部分，

• 上空间
• 超平面
• 下空间

梯度方向是函数增大的方向， - 梯度方向是函数减小的方向

3.1. 多面体 polyhedron

一个多面体 = 多个半空间相交

顶点 = 极值点 = 基可行解

3.2. 代数运算

3.2.1. 求基解

紧约束： 等式 对 顶点的确定起了作用， 成为紧约束，即 在这里不等式 变为等式

顶点定义： 紧约束数量 = dim()

等式约束本身就是紧约束，需要再选出部分非等式约束，组成 n 个约束

此时，求得的顶点是基解，但是由于缺少其他约束， 因此不是可行解

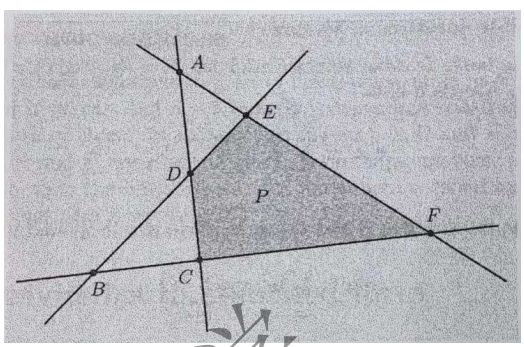
1. 线性约束数量 为 m , 变量数量为 n
2. M < n
3. 此时将 n - m 个 $ x_i \geq 0$ 变为紧约束，可以求解了

求出的 x 是基解 ， 即所有线段相交的节点

$$Ax = b \\ \begin{bmatrix} B & N \end{bmatrix} \begin{bmatrix} x_B \\ x_N \end{bmatrix} = b \\ Bx_B + Nx_N = b \\ Bx_B = b \rightarrow x_B = B^{-1}b$$

B 是基变量， N 为非基变量

3.2.2. 基解退化

3.2.2.1. 几何

其他约束在这里也是紧约束，有一个新的约束也是紧约束，是多余的紧约束， 反映在代数中有一个基解为 0 .

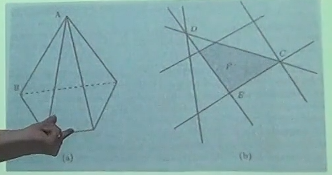
3.2.2.2. 代数

多个基 可能会对应一个基解

= 》 变换不同的解，但是相交的节点相同

3.2.2.3. 基解与节点坐标关系

3.3. simplex methed

	$x_B^T$	$x_N^T$	rhs
$x_B$	$B$	$N$	$b$
$r^T$	$0^T$	$c_N^T - c_B^T N$	$0^T$

---

	$x_B^T$	$x_N^T$	rhs
$x_B$	$I$	$B^{-1} N$	$B^{-1} b$
$r^T$	$0^T$	$c_N^T - c_B^T B^{-1} N$	$- c_B^T B^{-1} b$

$B^{-1} b$ 代表可行方向， 初始解开始可行，之后变换过程中，始终保持 rhs 为正

$c_N^T - c_B^T B^{-1} N$ 是最优方向

顶点数量为 $C_{n}^{n-m} = C_{n}^{m}$ ， 数量较大，选择一种有效的方式筛选点

1. 选择初始点
2. 从起始点 -》 最优点

对于线性规划， 是一个凸函数问题， 局部最优点 = 全局最优

1. 选择可行方向
2. 选择最好的方向
3. 方向上行动的距离

3.3.1. 可行方向

1. 开始 $ Ax = b$

2. 移动 x 到 下一个顶点， 为 $ x + \theta d$

3. 依旧满足顶点公式， $A(x + \theta d) = b$, 得到 $A \theta d = 0$

4. $$A = \begin{bmatrix} B, N \end{bmatrix} , d = \begin{bmatrix} d_B \\ d_N \end{bmatrix}$$

   其中 $ d_N$ 仅 修改 $ d_j$ ， $d_B$ 作为待修改对象（人为规定，不要问为什么）

   计算得到

   $$d_B = -B^{-1} * A_j$$

可行方向 $[d_B, d_N]$ ， 对于非退化解， 方向一定是可行，否则，不可行

3.3.2. 好的方向

原目标函数

$$C^T x ，转换为 C^T（x + \theta d)$$

reduced_cost 需要保证 $\bar{c}_j = c_j - c_B^T B^{-1} A_J$ , 结果值 要小于 0

3.3.3. 最优条件

1. 所有的基 向量大于 0
2. 所有非基变量的 reduced cost 大于 0 ，没有可以下降的非基 时候，

3.3.4. 行动的步长

$ cost = \theta * \bar{c} $ ，所以 $\theta$ 步长值 尽可能大

最大步长受限于 $X_B + \theta d_B$， 基变量的值需要满足非负变量

3.4. LP 基本矩阵

$x_B$ 是基变量， $ x_N $ 是非基变量

其中 $Ax = b , A = [B | N] , x =\begin{bmatrix} x_B \\ x_N\end{bmatrix}$

其中满足 $Ax = Bx_B + Nx_N = b$ ， 计算得到 $ x = [x_B ; x_N] = [B^{-1}b ; 0] $

式子可以改写为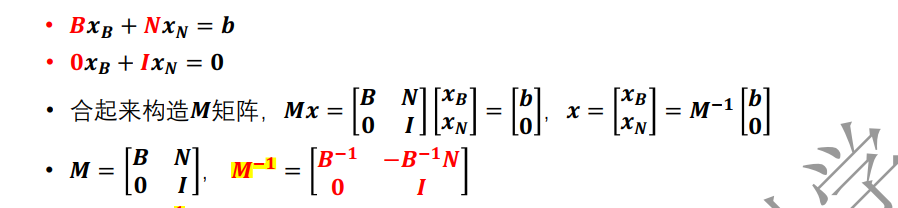

其中 M 成为基本矩阵

3.5. 两阶段 simplex method

原因 ： 当约束中不存在不等式约束 时， 不能增加新的变量， 构成基， 因此不容易找到初始可行解

方法： 使用两阶段单纯形法

4. 搜索算法

梯度方向 = 当前 $x$ 附近， 函数下降最快的方向

$$目标值的变化值 = f(x + \lambda \Delta x) - f(x) \approx \sum_j (\frac{\partial f}{\partial x_j}) (\lambda \Delta x) = \lambda \Delta f(x) * \Delta x)$$

内积最大的情况下， $\Delta f(x) = \Delta x$

1. max 变化值最大的 $\Delta x $ ， 取值 $\Delta x = \Delta f(x)$
2. min 变化值最大的 $\Delta x $ ， 取值 $\Delta x = -\Delta f(x)$

4.1. 有约束的搜索方向

1. 当 $ \Delta x = - \alpha_i^T$ 时候， 沿着可行方向的梯度无法下降，找到局部最优点，此时无法再下降
2. 否则，需要保持上图 1 中的约束条件

4.2. 解析解

做出一定的假设，使用解析解进行灵敏度分析

解析解是对输入参数的表示，原有输入参数中使用数值表示，是特定情况下的固定结果

即将原有的公式中的式子使用代数表示， 如图下所示：

5. dual method

pinal - > dual

reformation 一个心得问题，通过 relation 的方式实现

1. 提供新的求解方案
2. 提供另一个求解思路

5.1. legrengean relation

$$min \space x^2+y^2 \\ s.t. \space x+ y = 1$$

对不满足约束的情况增加惩罚 $p$, 得到

$$min \space x^2 + y^2 + p(x+y-1)$$

希望惩罚越来越小，所有 $()$ 内式子会趋近于 0

5.2. Pinal - > dual

$g(p) = c^Tx + p^t(b- Ax)$ 是松弛后的问题，每一 $g(P)$ 对应 原函数 $P$ 的下界，目标转换为对求解 $max \space g(p)$

然后通过推导，

$$min \space g(p)= min \space c^Tx + p^T b - p^T Ax = min \space( p^Tb + (c^T - p^T A)x)$$

因为 min 对 x 变量求最小值， 对 $P^T b$ 是常量，得到

$$min \space g(p) = p^T b + min \space (c^T-p^TA) x$$

因为 $x \geq 0$ ，所以，当 $c^T - p^TA \geq 0$ 时， min 可以取得最小值 0 ， 函数值取值为 $p^T b$

最终问题转换为

$$max \space p^T b \\ s.t. \space p^T A \leq c^T$$

5.2.1. 剩余形式约束转换

5.3. dualtiy theory

1. weak duality
2. strong duality
3. complementary slackness

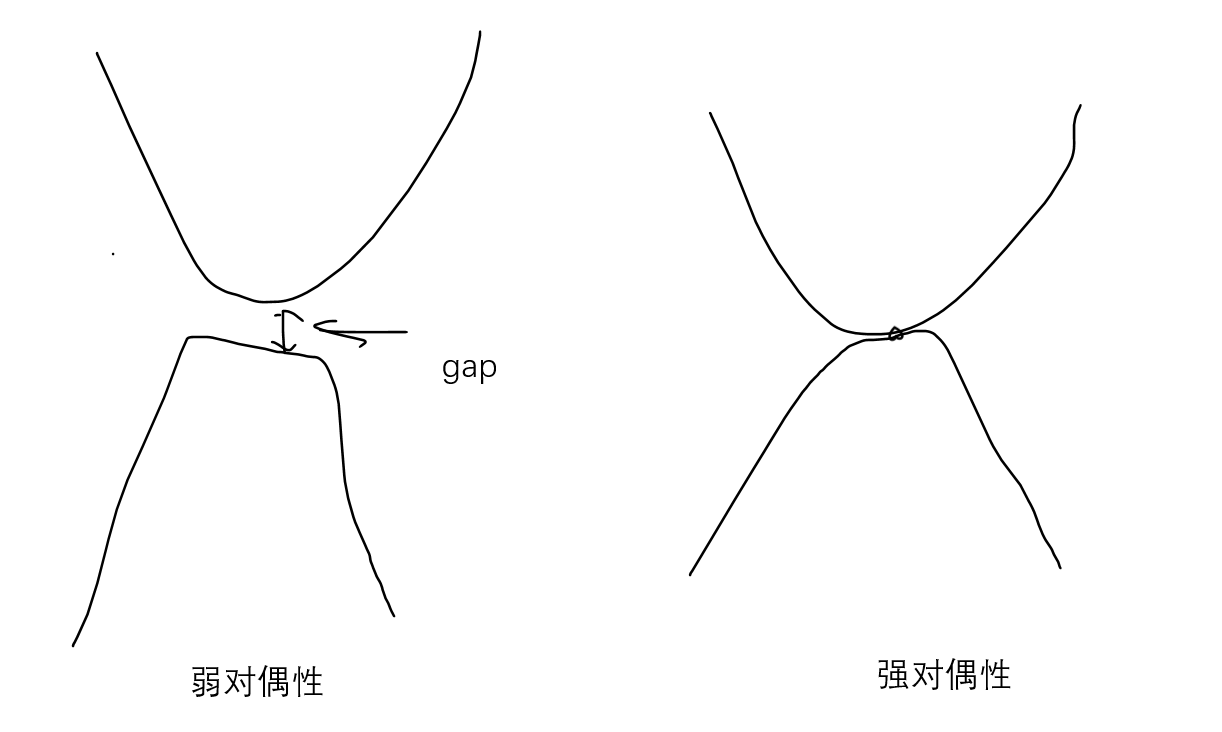
5.3.1. weak duality

$$c^T X > b^T w$$

5.3.2. strong duality

$$c^T x = c_B^T x_B \\ = c_B^T B^{-1} b\\ = w^T b \\ = b w^T$$

所以，得到 $w^T = c_B^TB^{-1}$

对偶问题可行 -》 原问题最优

5.3.3. 对偶理论

P 问题 f-b(feasible - bounded) 与 对应 D 问题的 f-b

5.3.4. 互补松弛理论

互补定义：

1. P 的松弛 * D 和可行解 = 0
2. D 的松弛 * P 的可行解 = 0

互补松弛理论： 满足互补松弛理论时 = 》 x 时最优解， w 也是最优解

5.3.5. KKT 条件

对于线性问题， 满足互补松弛理论，即可获得问题的最优解

5.4. 经济学变量

5.4.1. 互补松弛解释

​ 见 PPT

6. Integer programming

6.1. 分配问题

好的，我将为你提取图片中展示的三种指派问题（Assignment Problem）的 LaTeX 表达式。

---

6.1.1. 指派问题 (0-1 Assignment Problem)

目标函数：

$$\min \sum_{i = 1}^n \sum_{j = 1}^n c_{ij}x_{ij} \\ s.t. \quad \sum_{j = 1}^n x_{ij} = 1, \quad \forall i \\ \sum_{i = 1}^n x_{ij} = 1, \quad \forall j \\ x_{ij} \in \{0,1\}, \quad \forall i, j$$

---

6.1.2. 二次指派问题 (Quadratic Assignment Problem)

目标函数：

$$\min \sum_{i} \sum_{j} \sum_{k > i} \sum_{l \ne j} c_{i, j, k, l} \cdot x_{ij} \cdot x_{kl} \\ s.t. \quad \sum_{j = 1}^n x_{ij} = 1, \quad \forall i \\ \sum_{i = 1}^n x_{ij} = 1, \quad \forall j \\ x_{ij} \in \{0,1\}, \quad \forall i, j$$

分阶段分配：

1. 从 $x_{ij}$ 表示部门 $i$ 分配到地点 $j$
2. 从 $x_{kl}$ 表示部门 $k$ 分配到地点 $l$

$c_{i,j,k,l}$， 表示 $i ,j$ 在 $k, l$ 位置交互的 cost

$x_{ij} * x_{kl}$ 表示只有分配了这条链路， 才会产生 cost

---

6.1.3. 广义指派问题 (Generalized Assignment Problem)

目标函数：

$$\min \sum_{i = 1}^m \sum_{j = 1}^n c_{ij}x_{ij} \\ s.t. \quad \sum_{j = 1}^n x_{ij} = 1, \quad \forall i \\ \sum_{i = 1}^m s_{ij}x_{ij} \leq b_j, \quad \forall j \\ x_{ij} \in \{0,1\}, \quad \forall i, j$$

6.2. IP solution

1. LP 问题近似， 先视为连续问题，再求解
2. 启发式算法，求解质量无保证
3. 近似算法，求解质量具有保证

6.3. classic problem

6.3.1. 几何覆盖问题

6.3.2. 设施选择问题

1. 变量：有两类，
   1. 整数Y ，用于控制某个站点被建立，
   2. 实数X，表示建立的站点i 对 节点J 的服务比例

6.3.3. 网络问题

6.3.4. 车间调度问题

决策变量: $x_{j,k}$ 工作j 在设备K 上工作

约束：

1. $j, j’$ 约束 ， j 必须在 $j’$之前

   $$x_{j,k} + p_{j, k} \leq x_{j',k}$$

2. $j, j’$ 共同使用设备 $K $, 同一台机器不能同时服务同一个设备

   1. $j’$ 的开始时间需要小于 $j$的结束时间，严格约束

      $$x_{j,k} + p_{j,k} \leq x_{j',k} + M(1 - y_{j,j',k})$$

      当$y_{j,j’,k}$表示 作业 j 在 $j’$之前使用k ，值为1，表示可以使用

   2. 当$y_{j,j’,k}$ 为0 时， 约束生效，表示 $j’$必须在$j $之前完成

      $$x_{j',k}+p_{j',k} \leq x_{j,k}+ My_{j, j',k}$$

      $y_{j,j’,k}$， 表示 j ,j’ 在k 上具有冲突

      M 的约束作用， 当y 生效时，等式松弛，约束不起作用

      当y = 0 时，约束严格作用

6.4. 0-1 modeling

1. 0-1选择问题，是否选择

   

2. 关联约束

   

3. 组合中选择一个

   

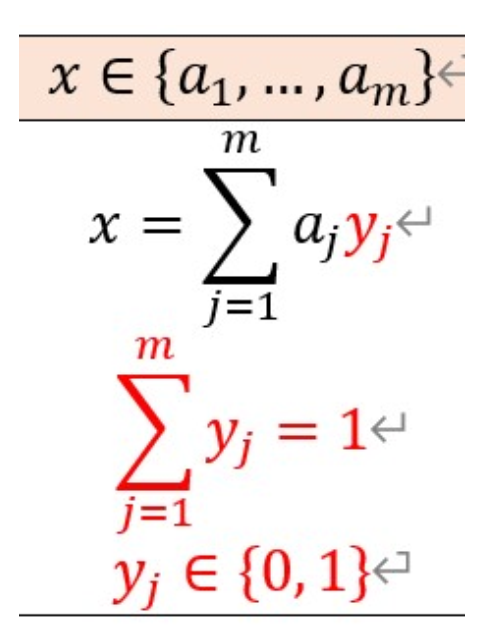
4. 选择约束条件